How Bitcoin Works

比特币经历了去年4月和11月的两次暴涨暴跌，已经不仅仅是 IT 男的玩物，而成为社会各界争论的焦点。不过关于比特币技术原理的文章大多是蜻蜓点水。过年与好基友们聊天时，大家提出了这些问题，希望读完这篇文章后能弄明白：

  1. 如何证实一次比特币交易，使其不可抵赖？
  2. 如何避免一个比特币花两次？
  3. 如果我一个人拥有全网的 10% 算力，是否有可能改写历史？
  4. 比特币交易为什么要等几十分钟？
  5. 比特币是如何保证数量有限（2100 万个）的？
  6. 如何保证每 10 分钟恰好挖出一个比特币？
  7. 一次挖出 0.1 个比特币是怎么回事？
  8. 一次交易 10000 个比特币，需要生成 10000 条交易信息吗？
  9. 比特币这么大的交易量，交易记录如何传输、保存？

（不了解比特币的请先看维基百科或度娘百科）

数字签名：比特币的基础

任何一种电子货币，首要问题是让交易不可伪造也不可抵赖。在日常生活中，交易往往是通过手写签名来实现的。在网络世界里我们用的是 ”数字签名“。《应用密码学》[3] 列出了数字签名的一些必要特征：

  1. 可信。签名的接收者相信签名者签了字。
  2. 不可伪造。是签名者而不是其他人签了字。
  3. 不可重用。不法之徒不能把签名移到别的文件上。
  4. 不可改变。签名之后文件的内容（交易金额）不能改变。
  5. 不可抵赖。签名者不能事后声称他没有签名。
    如果 Alice 有一个密码，告诉了 Bob，现在两个人都有这个密码了，这个密码现在属于谁，就说不清了。用传统方法很难想到一种在不依赖第三方的情况下满足上述5条的签名方式。1976年，Diffie 和 Hellman 的公开密钥密码学 [4] 使得两个陌生人可以在没有任何公共秘密的情况下实现秘密通信，这使得数字签名成为可能。

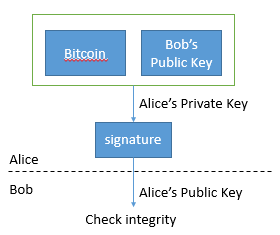
参与交易的两个人分别持有一对公私钥，公钥是公开的，私钥是自己持有的。一条明文信息可以用私钥加密，再用公钥解密（注意，跟加密通信不同）。Alice 要给 Bob 一个比特币，Alice 就把 “这个比特币（一串信息）给 Bob（Bob 的公钥）” 的信息用自己的私钥加密，得到的结果传给 Bob。Bob 拿到的就是一个比特币了。Bob 用 Alice 的公钥解密，证实这个比特币的有效性以及自己公钥的正确性。

CaptureCapture

这种做法满足数字签名的五个特征 [3]：

  1. 可信。Bob 用 Alice 的公钥解密，证实这是由 Alice 签名的。
  2. 不可伪造。只有 Alice 知道她的私钥，而已知公钥是无法推出私钥的。
  3. 不可重用。得到的结果是 “比特币 + Bob 公钥” 的函数，不能由其他比特币或者 Bob 以外的人的公钥得出。
  4. 不可改变。如果结果有任何改变，Bob 就无法用 Alice 的公钥解密。
  5. 不可抵赖。Bob 不需要 Alice 或任何第三方就能用 Alice 的公钥解密，验证 Alice 的签名。
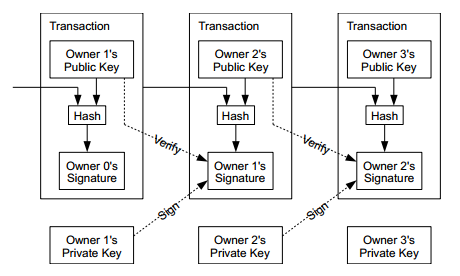
    第五个特征有一些问题。如果 Alice 事后说这不是我的公钥，怎么办？在传统的数字签名机制中，Alice 公钥的不可抵赖性由可信的第三方解决；但在比特币这样一个完全去中心化的系统中，不允许也不需要第三方。事实上，Alice 的公钥就在比特币里。考虑 Alice 这个比特币的来源，先不考虑自己挖出来的情况，那么就是别人给的，则在上次交易中，Alice 的公钥就已经存储在比特币中。

比特币 = 交易历史链

事实上，比特币就是由上述交易过程组成的数字签名链。只要比特币的 “最初来源” 是可以验证的，整个比特币，也就是这个交易过程，就是可验证的。

由于数字签名和验证签名是比较耗计算资源的，我们不希望一个比特币经过长时间流通后，消息体越来越大，每次需要签名的内容越来越多，因此每次交易时签名的事实上是 “原来的比特币 + 买主的公钥” 的 Hash 值。用于密码学的 Hash 是一类单向函数 f(A) = B，已知 B 很难求 A，已知 A 也很难找到 A’ 使得 f(A) = f(A’)。这样便在不降低安全性的前提下提高了性能。

CaptureCapture

杜绝两次消费

细心的读者也许已经发现，上述签名机制不能阻止一个人两次消费同一比特币。要想杜绝两次消费，必须检查所有交易历史，证实这次交易之前这个比特币没有被消费过。最容易想到的解决方案是引入一个可信的中心机构，保存所有交易历史，并对每次新交易做检查。但是这样的中心机构违反了比特币完全分布式的设计理念。在比特币系统中，每个人都能获取所有交易历史并做检查。

公开交易历史会不会破坏匿名性呢？不会。比特币的隐私模型与传统金融机构不同。如下图所示，比特币尽管所有交易公开，但比特币持有者（Identities）并不包含任何现实世界的识别信息，只是一对公钥和私钥和一个 34 位的比特币地址。

CaptureCapture

历史只能有一个。让世界上所有比特币使用者同意唯一的交易历史，正是电子货币设计的难点和比特币的创新之处。由于比特币是匿名货币，“一人一票” 不能通过识别真实身份的手段实现。一个 IP 地址一票更是扯淡，开发过投票网站的都深受不断更换 IP 的刷票机器的困扰。比特币的做法是，一个 CPU 一票！让计算机用穷举法解公认的数学难题，解出一个题就算一票。不过，现在 GPU、FPGA 乃至 ASIC 的刷票能力远远超过了 CPU，因此很多号称 “只能用 CPU 挖矿” 的电子货币如雨后春笋般冒出来。

每个 CPU 一票

比特币所出的难题形式很简单：寻找一个 Nonce 值，使得 “Nonce 值 + 上次 Hash 值 + 欲证实的交易信息 + 时间戳 + 目标”（这称为一个块，block）的 hash 值小于或等于某个给定的阈值（称为目标，target）。hash 函数使用的是 SHA-256，结果是一个 256 二进制位的整数。

SHA-256 是密码学安全的 hash 函数，这意味着 Nonce 值的微小变化将导致 hash 值面目全非，给定一个 hash 值也无法反推出 Nonce 值。因此，寻找 Nonce 值跟买彩票差不多，就是随机试验 Nonce 值，每次试验都会得到一个基本上是随机的 256 二进制位整数，如果小于等于目标，则就算解决了难题。相比最大的256位整数，目标是一个非常小的数，例如我写这篇文章时的目标是

1
0000000000000001A36E00000000000000000000000000000000000000000000

这意味着平均每尝试 1.1259018e+19 次，才能找到一个新块。

当某个人宣布解决难题时，就要广而告之，世界上的其他人都会以他生成的这一新块为基础继续尝试。

CaptureCapture

每个人手里的块构成一棵树（当然有可能只是一条链）。收到的新块总是放在树的叶子节点。最长的树根到叶子那条链就是被承认的那条链。寻找下一块时，总是以这条最长链的叶子节点的 hash 值为基准。

在比特币的世界里，大家只承认最长的链（block chain），也就是最长链中包含的交易信息才是有效的。大家公认的第一块（genesis block）是硬编码在比特币软件里的，由于最长链准则，事实上这一块已经不再需要硬编码了，因为从一个新的 genesis block 开始，生成一条比现在还长的链，从概率上已经不可能。

篡改历史的尝试

如果一个人试图篡改 N 个块以前的交易历史，就必须从那个被篡改的块开始，生成一个比 N 更长的链，否则他的篡改将不会得到承认。注意，这种篡改是无法生成非法的交易记录的（因为交易记录只有持有私钥才能生成），只可能隐藏一些合法的交易记录，或者篡改自己的交易记录（例如本来是给 Alice 的交易改成给了 Bob），因此篡改历史的危害是有限的。下面将说明，只要“魔高一尺，道高一丈”，也就是破坏者的计算能力明显小于全网算力的一半，他就几乎没有可能篡改历史。

破坏者与比特币网络中其他诚实守信的人比赛谁生成的链更长。每个时间单位，破坏者的算力是 p，生成一块的概率是 p；诚实人的算力是 q，生成一块的概率是 q。破坏者每生成一块记作 +1，诚实人每生成一块记作 -1，则这就是经典的随机游走问题。当 p < q 时，随着时间推移，破坏者获胜的概率呈指数降低。[1] 表明，当 p = 1/10 * (p+q)，即破坏者是全网算力的十分之一时，在诚实者制造出5块后破坏者仍能赶上或获胜的概率小于 0.1%；即使破坏者算力达到全网的 30%，在诚实者制造出24块后破坏者仍能赶上或获胜的概率也小于 0.1%。

也就是说，只要一个交易被写入某一块后，比特币网络已经制造了足够多的块，则这个历史几乎永远不可能被篡改了。因此一个交易只需等待足够长的时间即可确保生效。在实际中，这个时间往往是60分钟，即制造出6块所需的时间。

稳定块的生成速度

目标（target）被设计为全网每10分钟制造出一个新块。这个时间足够短，以便链能以合理的速度增长，降低交易确认所需的时间；这个时间足够长，以便造出新块的人广播给其他正在挖矿的人，让他们从新的起点开始。

参与挖矿的人有时多有时少，计算机的计算能力也在不断提高，目标一成不变显然是不行的。比特币的设计是，每生成 2016 块（大约需要两个星期），就调整一次难度，即改变目标（retarget）。如果每10分钟恰好生成一块，则生成2016块恰好需要两周。比特币客户端比较生成这 2016 块所花的实际时间和 “两个星期” 的目标，如果所花时间长于两周，则增加难度，即减小目标；反之降低难度，即增加目标。为防止目标颠簸，规定每次目标的变化幅度不能超过4倍，即新目标不小于原目标的25%，不大于原目标的400%。

事实上，如下图所示，比特币网络的算力大多数时候是不断增加的，此时生成一块所需时间少于10分钟，难度也不断增加。（更多图表）

speed-everspeed-ever

目标以难度（difficulty）的形式存储在每个块里。难度 = Pool Difficulty / Target，其中 Pool Target 是个256位整数，其前32位为0，后面都是1。

目标的自适应变化会不会给试图篡改历史的人以可乘之机呢？破坏者如果先算慢一些，等目标降下来了再加速，是不是会有更大的机会超过诚实者？不会。证明思路：第一次 retarget 之前结论是显然的，第二次 retarget 之前可以用二次函数证明不可能，之后的 retarget 可以用数学归纳法和二次函数证明不可能。

比特币的分割与合并

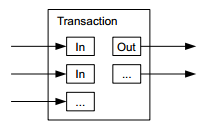
如果每个比特币只能作为一个整体来消费，并且每次交易只能消费一个比特币，则做大宗或者小额交易也太不方便了。因此比特币在交易时是可以分割或合并的。事实上，每个交易可以有多个输入和两个输出（为简单起见，前面讲解数字签名链时假定只有一个输入和一个输出）。多个输入是指可以合并多个比特币。两个输出，一个是付给比特币买家的比特币金额，另一个是退还给比特币卖家的找零。显然，输入与输出的比特币数应当守恒。

CaptureCapture

比特币并不是无限可分的。比特币的最小单位是 1/100M（亿分之一），以比特币的创始人 satoshi 命名。

交易历史的裁剪

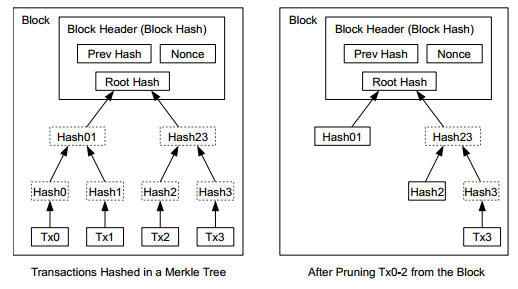
我们看到整个比特币交易历史都存储在每个比特币交易节点中。磁盘空间即使现在不是问题，将来也一定会成为问题。比特币采用了 Merkle Tree 使得交易节点可以随时移除部分交易历史而保持整条链的完整性。

如下左图所示，各个交易分别算出 hash 值，这些 hash 值两两配对算出 hash 值，再两两配对……直到算出根 hash。树中每个节点要么是原始交易信息，要么是一个 hash 值，要么两个孩子节点都存在。这样我们可以随时删除任意选定的原始交易信息以节约磁盘空间。下右图是删除了 0,1,2 三个交易信息后的 Merkle Tree。极端情况下，我们可以删除所有原始交易信息，只留下 Root Hash。

CaptureCapture

如果裁减掉所有交易信息，一个 block header 是80字节，按照10分钟一块的速度计算，这条链每年只会增长 4.2MB，完全不是问题。

可扩放性 (Scalability)

VISA 每秒大约处理 2000 次交易，高峰时段每秒能处理 10000 次交易。而直到 2012 年底，比特币网络平均每秒才处理 0.5 次交易。[6]

每个交易大约需要 0.2KB ~ 1KB，按平均 0.5KB 计算 [6]，要每秒处理 2000 次交易，需要 7.8Mbps 的带宽，这对服务器来说自然不算什么。因此在网络通信方面比特币能轻松支持 VISA 规模。

一个 Core i7 CPU core 每秒能做 8000 次数字签名检查，而每个交易平均需要做两次数字签名检查（平均每次交易有两个输入 [6]，每个输入需要检查一次数字签名），也就是单核 CPU 每秒就能处理 4000 次交易，达到了 VISA 规模。

因此，作为一个交易系统比特币的可扩放性是没有问题的。但如果想把比特币的最长链算法用于其他类型的网络服务，也许就要考虑可扩放性问题了，最好减少在整个网络中广播的消息数量。

受控的比特币发行

讲了这么多，还没说比特币是从哪里来的呢。比特币设计的一个巧妙之处是，保护交易历史的 “每个 CPU 一票” 机制，同时也是比特币发行的机制。每解决一道难题，也就是算出一个 block，就能得到一定数量的比特币（注意，不是一个比特币）。这使得在比特币发展初期和以后很长一段时间内，为了获得比特币回报，大家会投入大量算力来“挖矿”。挖矿的人越多，算力越强，试图篡改历史的破坏者就越难得逞。

为了控制货币发行，比特币奖励是越来越少的。最开始（2009 年），每算出一块，能得到 50 比特币。2009 ~ 2013 年共发行 1050 万个比特币，占比特币发行总量的 50%。在 210000 块之后，也就是从 2013 年开始，奖励减半，即每算出一块能得到 25 比特币。2013 ~ 2017 年共发行 525 万个比特币，占总量的 25%。此后大约每4年，奖励都会减半（以 1 satoshi 为最小单位，向下取整），直到公元 2140 年，每算出一块的奖励从 1 satoshi（1/100M 比特币）降到 0，21M 个比特币发行完毕，再也不会有更多的比特币了。

有人可能会问，我们挖矿都是获得 0.1 个、0.01 个比特币，从来没有得到 25 个比特币啊？那是因为独自挖矿太难了，得到 25 个比特币固然可观，但就目前的难度而言，平均需要尝试 1.1259018e+19 次才能找到一块（平均每11天难度还会增加30%！）。因此独自挖矿是高风险的，一般都是加入矿池，矿池内部分配任务，风险与收益均摊，就把碰运气的事情变成了比特币收入基本与算力成正比的稳定投资。有的矿池在挖到比特币（一次就是25个）时按照参与者投入的算力均摊；有的矿池不管挖没挖到比特币，都按照投入的算力结算。

事实上，如果比特币的难度控制（retarget）按照预想的工作，2018 年 90% 的比特币将会发行出来，2030 年 99% 的比特币将会发行出来。（每年预计发行的比特币数量：传送门）几十年后，如果比特币仍然在流通，大家投入算力可能就不是为了挖矿了，而是保护交易历史。在比特币的世界里，交易历史就是一切，因此比特币持有者会投入算力来保护自己的财富。

比特币能成为人类历史上第一种流行起来的电子货币，与其巧妙的算法设计是分不开的。如果在设计分布式系统时能受到比特币的一点启发，善莫大焉。

参考答案

  1. 如何证实一次比特币交易，使其不可抵赖？基于开放密钥密码学的数字签名。
  2. 如何避免一个比特币花两次？最长链，一个 CPU 一票，交易历史完全公开。
  3. 如果我一个人拥有全网的 10% 算力，是否有可能改写历史？几乎不可能改写一小时以前的历史。
  4. 比特币交易为什么要等几十分钟？为了生成足够多的后续块，在概率意义上保证交易不被篡改。
  5. 比特币是如何保证数量有限（2100 万个）的？每经过 210000 个块，生产出每块的奖励减半，因此比特币的发行量随时间变化是等比数列。
  6. 如何保证每 10 分钟恰好挖出一个比特币？这个问题的提法不对，不是挖出一个比特币，而是挖出一块。而且也不能保证，只是通过难度的动态调整（retarget），使得全网大约每 10 分钟生产出一块。
  7. 一次挖出 0.1 个比特币是怎么回事？加入了矿池，收益均摊。
  8. 一次交易 10000 个比特币，需要生成 10000 条交易信息吗？不需要，比特币可以合并。
  9. 比特币这么大的交易量，交易记录如何传输、保存？交易历史可以裁剪，网络带宽和验证数字签名所需的 CPU 目前不是瓶颈。

References

  1. https://bitcoin.org/bitcoin.pdf
  2. Bitcoin wiki: https://en.bitcoin.it/wiki/Category:Technical
  3. Bruce Schneier, “Applied Cryptography: Protocols, algorithms and source code in C” (Second Edition)
  4. W. Diffie and M. E. Hellman, “New Directions in Cryptography”, IEEE Transactions on Information Theory, 1976
  5. http://bitcoin.sipa.be/
  6. https://en.bitcoin.it/wiki/Scalability
  7. https://en.bitcoin.it/wiki/Controlled_Currency_Supply

Comments

▲